(C++) 백준 3020 : 개똥벌레 (feat. imos 알고리즘)
문제
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다.
아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)
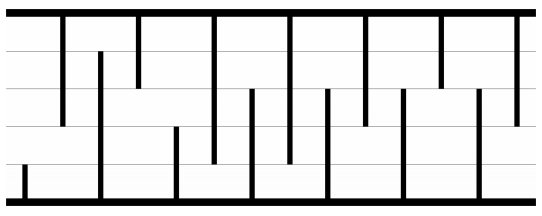
이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)

하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
출력
첫째 줄에 개똥벌레가 파괴해야 하는 장애물의 최솟값과 그러한 구간의 수를 공백으로 구분하여 출력한다.
예제 입력 1
|
6 7
1 5 3 3 5 1 |
예제 출력 1
|
2 3
|
예제 입력 2
|
14 5
1 3 4 2 2 4 3 4 3 3 3 2 3 3 |
예제 출력 2
|
7 2
|
나의 풀이:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int N, H;
cin >> N >> H;
vector<int>imos(H+1);
for (int i = 0; i < N; i++) {
int a;
cin >> a;
if (i % 2 == 0) {
imos[0]++; //입장으로 생각
imos[a]--; //퇴장으로 생각
}
else {
imos[H - a]++; //입장으로 생각
imos[H]--; //퇴장으로 생각
}
}
int now = 0;
for (int i = 0; i < H; i++) { //누적합 계산
now += imos[i];
imos[i] = now;
}
int Min = *min_element(imos.begin(), imos.end()-1);
int cnt = 0;
for (int i = 0; i < H; i++)
if (Min == imos[i]) cnt++;
cout << Min << " " << cnt;
return 0;
}
이 문제는 Binary Search로 푼 사람들이 많은 것 같은데 나는 imos 알고리즘을 사용하여 풀이해보았다.
얼마전에 imos알고리즘을 처음 접해보았는데, 올해 카카오, 요기요 코딩테스트 등 종종 출제되었다고한다.
imos 알고리즘이란?
누적합을 효율적으로 처리하는 알고리즘으로 입장과 퇴장만 기록한다는 특징이 있다.
"0시부터 T시까지 운영하는 장소에 N명의 사람이 입장과 퇴장을 반복할 때
각 시간에 대해 존재했던 사람이 몇명인지 혹은 가장 많은 사람이 존재했을 때의 손님 수는 몇명인지"
등의 상황에서 사용할 수 있는 개념이다.
해당 백준 문제에서 동굴의 높이를 운영 시간으로, 동굴의 깊이를 입장한 사람의 수로,
장애물을 입장한 시간으로 생각한 뒤 짝수, 홀수만 구별한다면 위의 상황과 동일하다고 볼 수 있다.