[알고리즘] MST(최소신장트리), 크루스칼(Kruskal) 알고리즘이란?

 

✔️ MST란?

MST는 Minimum Spanning Tree의 약자로, 그래프에서 최소 비용으로 모든 구간을 연결한 Tree(최소 신장 트리)를 말한다.

무향 연결 가중 그래프에서 간선의 가중치의 합이 최소인 신장(Spanning) 트리(Tree)이다.

MST의 특징

• MST는 Tree이기 때문에, Cycle이 존재하면 안된다. 따라서 신장 트리는 정점의 갯수가 n개일 때, 간선이 n-1개가 된다.
• 답은 여러개가 될 수도 있다.

✔️ 크루스칼(Kruskal)이란?

크루스칼(kruskal) 알고리즘은 MST를 구하는 대표적인 알고리즘이다.

크루스칼 알고리즘의 시간복잡도는 O(nlog𝑛)이다. 여기서 n은 연결되는 간선의 수를 의미한다.

 

Kruskal 알고리즘의 과정

1. 가중치 값을 기준으로 정렬(sort)
2. Union Find 자료구로를 이용하여 간선 선택

Union Find 자료구조가 무엇인지 모른다면? 👉 [알고리즘] Union Find(서로소 집합)란?

[알고리즘] Union Find(서로소 집합)란?

 

Kruskal 상세 과정

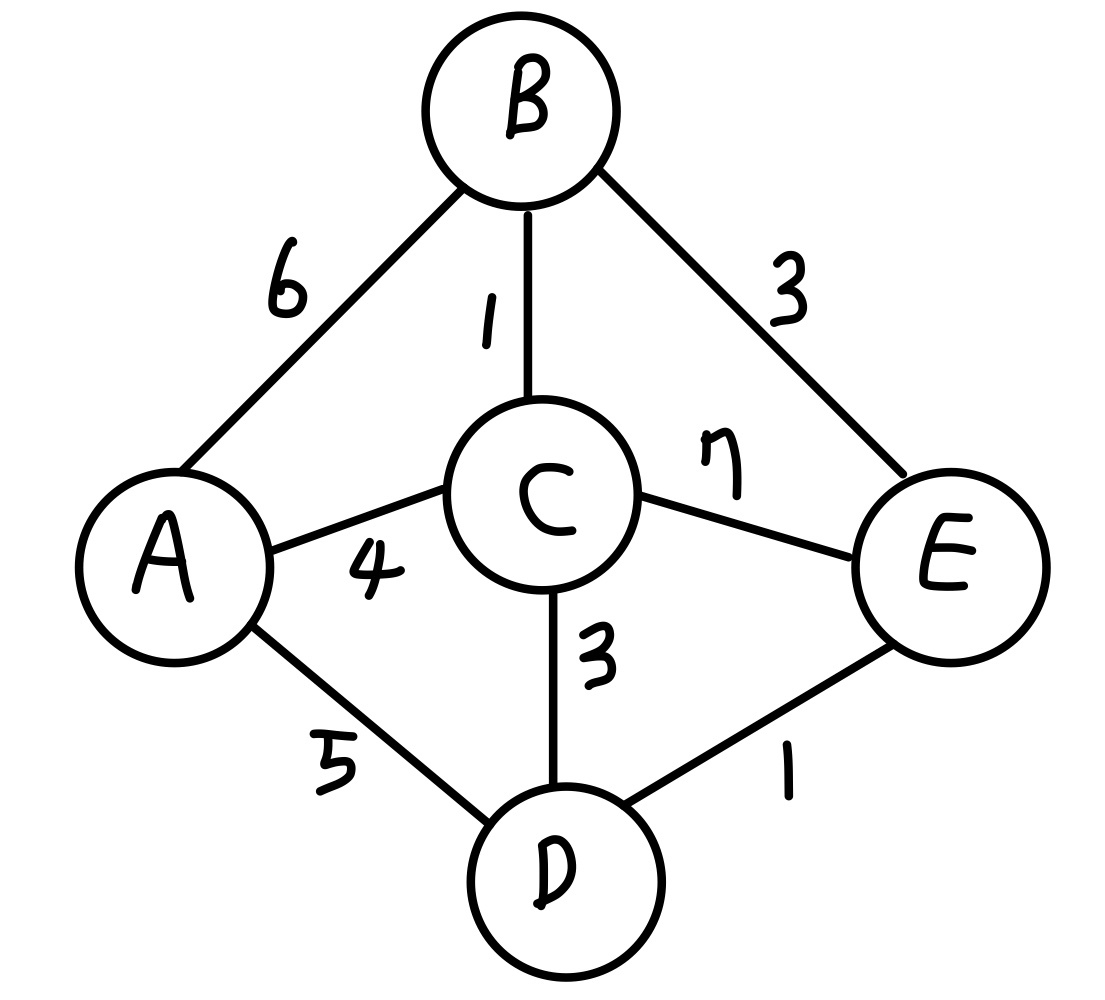
과정 1 : 그래프 정의하기

먼저 아래와 같은 그래프를 하드코딩한다.

여기서는 struct 구조체를 사용하여 {노드, 노드, 간선 가중치} 구조의 노드를 정의한다.

 

#include <iostream>
using namespace std;

struct Node {
	char v1, v2; //연결되는 노드
	int val; //간선의 가중치
};

Node node[8] = {
	{'A', 'B', 6},
	{'A', 'C', 4},
	{'A', 'D', 5},
	{'C', 'B', 1},
	{'C', 'D', 3},
	{'C', 'E', 7},
	{'E', 'B', 3},
	{'E', 'D', 1},
};

 

과정 2 : 정렬하기

생성된 node 배열을 가중치(val)을 기준으로 정렬한다.

이때, compare 메소드를 정의하여 정렬(sort)한다.

#include <iostream>
#include <algorithm>
using namespace std;

struct Node {
	char v1, v2; //연결되는 노드
	int val; //간선의 가중치
};

Node node[8] = {
	{'A', 'B', 6},
	{'A', 'C', 4},
	{'A', 'D', 5},
	{'C', 'B', 1},
	{'C', 'D', 3},
	{'C', 'E', 7},
	{'E', 'B', 3},
	{'E', 'D', 1},
};

bool compare(Node n1, Node n2)
{
	return n1.val < n2.val;
}

int main()
{
	sort(node, node + 8, compare);

	return 0;
}

정렬이 완료된 후 node 배열은 다음의 형태를 갖는다.

 

 

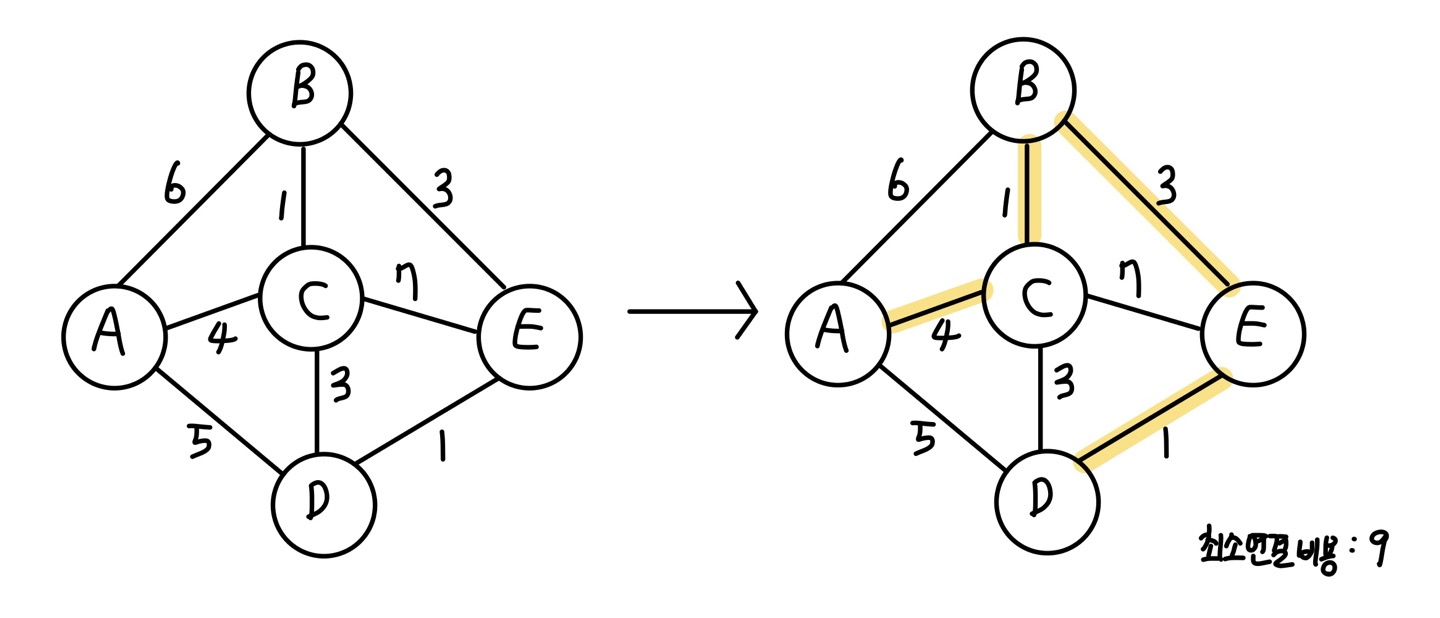
과정 3 : 간선 선택하기

1중 for문을 돌리면서 MST가 될 간선을 결정한다.

이때 맨 앞에 있는 C-B 간선이 MST의 간선으로 채택되며, 노드 C와 노드 B는 같은 그룹이 된다. (UnionFind)

 

과정 4 : 간선 선택하기

E-D 간선이 선택되고, E와 D가 같은 그룹인지 먼저 확인한다. (Union Find 사용)

E와 D는 다른 그룹이기 때문에 같은 그룹으로 만들고 MST로 채택한다.

 

 

과정 5 : 간선 선택하기

E-B 간선이 선택되고, E와 B는 다른 그룹이므로, 같은 그룹으로 만들고 MST로 채택한다.

 

과정 6 : 간선 선택하기

C-D 간선이 선택되고, C와 D는 같은 그룹이다.

같은 그룹인 노드를 연결하면 Cycle이 발생한다. 따라서 C-D 간선은 MST로 채택하지 않고 넘어간다.

 

 

과정 7 : 간선 선택하기

다음으로 A-C 간선이 선택되고, A와 C는 다른 그룹이기 때문에 같은 그룹으로 만들고 MST로 채택한다.

 

총 5 - 1 = 4개의 간선이 채택되어, MST가 완성되었다.

 

 

💻전체 소스코드를 살펴보면 다음과 같다.

#include <iostream>
#include <algorithm>
using namespace std;

struct Node {
	char v1, v2; //연결되는 노드
	int val; //간선의 가중치
};

Node node[8] = {
	{'A', 'B', 6},
	{'A', 'C', 4},
	{'A', 'D', 5},
	{'C', 'B', 1},
	{'C', 'D', 3},
	{'C', 'E', 7},
	{'E', 'B', 3},
	{'E', 'D', 1},
};

bool compare(Node n1, Node n2)
{
	return n1.val < n2.val;
}

//Union Find 코드
char parent[200];

char getParent(char ch)
{
	if (parent[ch] == 0) return ch; //자신이 root인 경우
	return parent[ch] = getParent(parent[ch]);
}

bool setUnion(char ch1, char ch2)
{
	char p1 = getParent(ch1);
	char p2 = getParent(ch2);
	//다른 그룹인 경우
	if (p1 != p2) { 
		parent[p2] = p1; //ch2 그룹 root의 부모를 ch1 그룹의 root로
		return true; 
	}
	//같은 그룹인 경우
	return false;
}

int main()
{
	//가중치를 기준으로 정렬하기
	sort(node, node + 8, compare);

	//MST 만들기
	int cnt = 0; //선택된 간선의 수 -> 노드의 수 - 1이 되어야함 
	int sum = 0; //선택된 간선의 가중치의 합
	for (int i = 0; i < 8; i++)
	{
		//그룹이 다른 경우, 사이클이 생기지 않는 경우만 연결
		if (setUnion(node[i].v1, node[i].v2)) {
			sum += node[i].val;
			cnt++;
		}
		if (cnt == 4) {
			cout << "최소 연결 비용 : " << sum;
			break;
		}
	}
	return 0;
}

 

 

크루스칼 알고리즘을 활용한 문제(예시)와 풀이는 다음에서 확인할 수 있다.

👉 https://nayoungs.tistory.com/entry/C-%EB%B0%B1%EC%A4%80-1647-%EB%8F%84%EC%8B%9C-%EB%B6%84%ED%95%A0-%EA%B3%84%ED%9A%8D-MST-Kruskal

(C++) 백준 1647 : 도시 분할 계획 (MST, Kruskal)